钦定古今图书集成历象汇编历法典

　第五十七卷目录

　历法总部汇考五十七

　　新法历书七〈月离历指三〉

历法典第五十七卷

历法总部汇考五十七

新法历书七

月离历指三

《三圜比例说》第二十五

三。圜者，日一、月二、地三，皆为圜体。历家先求其比例 大小远近之数，为测验推算之基本。此诸数者，骤言 之，似出恒闻习见之外，故是信情所不能及。如太阳 之体，目视之不过数寸耳。曰大于地球之体一百五 十倍，谁即信之？月与日，人目不能别其大小，日月之 体，小于日几千倍，谁即信之？然从古至今，诸历名家， 测验推算，以理以数，反复论定，咸宗斯指。迨用以求 七政行度、交食、合会一切诸法，非此不合，即又无能 不信也。先臣邓玉函定着一书，甄明此术，引入《月历》， 疑于过繁。今择其要切者著于篇，凡为题十，借题一， 共十一题。

借题

借题者，不属本论，借外论以为义，据下文所必须也。

一、“地体”为《圜球》〈见表度说及地球图说〉

二、地球在《大圜》之中心〈见测天约说及表度〉

三目见物，仅能定其似，大小目接于物，物之诸分皆 发本象来至于目，目则全收其象云“收象”者，非在目 之外郛也。晴本圜球，有同鸟卵，重重抱裹。收象之处， 在其最中，为之瞳心。若目视物之四周，则四和线发 来至瞳心，合而成角，为角体之形。若视物之两端，则 两腰线发来至瞳心，合成三角面之形。凡角之末锐。

图

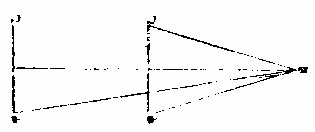
必在瞳心名为视角角之大小称物之大小苦视角极微目不见物乃不能定其大小若视角过大则目眶所限不能尽角之广必移目两视乃得全见四同是一物在近见大在远见小以三角形之理明之如图甲乙同底若腰长

则底之对角必小。

“《甲乙》线” 以近远生目中，视角大小。

五、未定物之近远。目不能定其实大小，近远大小视 法，皆有比例。

六、近远两物，大小不等。若小者在近，大者在远，而视 角等，则目定，其大小亦等。

如日月之视径等，不知者疑其大小亦等。不能辨其远近。不能分似大实大故也。

七、《有光之体》，体之各分，皆能发光。

八、《光景之限难分》。凡有光之体，体之四周，皆有切气， 借光于体，亦可当有光之体而发浮光。故表景之末， 渐至虚淡，其浓实者，是“正光之景，其虚淡者，则浮光 之景。”

第一题：《测太阳太阴之视径》。〈凡八法：〉

“月去人近，日去人远”，先得月之视径及其视差，乃可 求日之大小远近。故先求月之视径。视大小之度，在 瞳心之视角，角之度分，即对弧之度分。人目在大圜 之心。

或在地心，或在地面，今此无分，不烦别论。

则天上度分，为目所定视大小之度分，故论日月视 径，皆用周天度。如曰“半度”，曰“三十分”，则周天七百二 十之一也。

第一法

古用《壶漏法》：

《西土》，《厄日多》国人所创。

从午正初启溜，至明日午正止。权其废水，得重若干。 次候月初升启溜。〈用原壶原水〉升竟则止。权其废水，得重 若干。次用三率法，先水若干，得九十六刻；后水若干， 得几何刻分为月径全升之时。再用三率法，得为全 周之几何。古亚利谷以此定为七百二十一分之一， 约为二十九分五十九秒。　古依巴谷定为三十三 分一十四秒，加白蜡定为三十六分。

“以上三术，未定太阴最高，庳自行近远，数多不合。又 水漏法参差之缘甚多，难于切准，或用沙漏自鸣钟， 其定太阴升降，与此同法。”以下诸法，测日多通用。

第二法

《后此历》家谓“太阴出入升降，舒亟无恒，或经时不行。”

太白升降有时，迟至一刻，不见运动。

或俄然陨坠。凡此皆清《蒙》之气所为也。则蒙气之中。 未可以行定时。以时定径。更立法植物为表。或版或 墙。在目之南表之西际以当午线。目在表北。依不动 之处。候月之西周至于午线。便须启溜。

“或水或沙” ，或自鸣钟。

候体全，过午止。溜考之，得时得度，与前法同。

第三法

图

上法测用月午可免清蒙之差然月行自有迟疾以时定径亦未能得其实经度也苐谷别立一法两人用两象限仪候月正午同时并测一测其上弧距地平若干一测其下弧距地平若干两数之较为月半径如总积六千三百○○

图

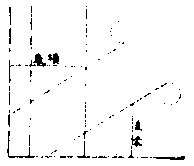
年为万历十五年丁亥在其本地测得上弧距地一十五度二十分下孤距地一十四度四十分其较三十四分为目之似径度分

第四法

或用横直二表及景符直表平圭定上弧之高横表立圭定下弧之高相减得

径。

用表求高法见《测量》十卷。

第五法

两人同时同测，一以表景求高，一以象限求高，两高 之较，日月之半径也。

表景得上弧之高，象限得心之高。

图

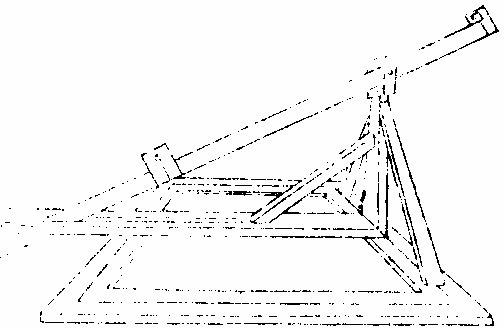
第六法

苐谷及其门人刻白尔借古依巴谷多禄某法为木候仪先作木架立柱高与人等柱端为两运之轴一周转一上下

木为长衡三分之一在前二在后而入之轴上下左右无所不可至也衡之两

端各立一表，上表中心为圆孔，径二三分，下表与上 表同心，从心作圈，与上孔等。圈之外更作数平行圈， 两表之间为《景箫》。

法见《测量全义》十卷《新仪解》。

以束上景，而致之下表也。箫之下端剡寸许，缺之，令 旁见下表之景圈。或不用景，箫则设之幽室，独直上 表其外，以受日光。达于下表。室须黝黑，绝无次光。

“日月火所照，皆为正光” ，所照之外，而能见物，皆其次光也。

图

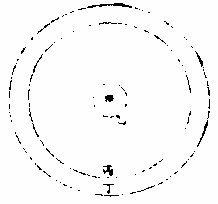
乃得实景用时以上表承日光在下表则成圆形必合一圈

不合更作合者

如甲为下表之心甲乙圈与上孔等光之半径为甲丁取丙丁与甲乙等作丙圈即甲丙与乙丁亦等乙为日周其光至丁甲为日

心，其光至丙。是两表相距若干。因生大甲、丙之光若 干。用三角形法，求甲、丙于两表之距度，得几分，即见 日视角之度分。法表相距之几丈尺与全，若甲丙与 视角之切线。

查八线表取数

刻白尔，用此候得冬至日径，为三十一分半，夏至减 一分有奇，为是三十分，则半度也。《苐谷》之表间一丈 四尺，冬至得三十一分。

较刻《白尔》为少半分。

《系日》视径有大小，则为日之近远。既有近远，安得无 最高、最庳？大不恒在冬至，小不恒在夏至？而有运移， 安得最高、最庳，不有运移？假令不信日有自行，则视 径大小，无义可说。

若无本仪，则于密室中穴墙壁。以版如上表法承日。 别用平表。准下表以受光。诸法同前。作孔或方或撱。 无所不可。

若测月径，光淡难分，则上表之孔特宜加大刻白尔。 所测为月平。〈两留际也〉距地少至二十九分半强，多至三十一分十二秒弱。〈光淡难定故〉极近距地少至三十二 分强，多至三十四分一十八秒弱。

第七法

以远镜求冬夏二至两径之差法木为架，用远镜一 具，入于定管，量取两镜间之度。后镜之后有景圭，欹 置之。管与圭皆因冬夏以为𫖯仰其管，圭之相距则 等。至时从景圭取两视径，以其较较全径，为二至日 径之差。

第八法

测月求附近两恒星，一左一右，与月参直。以月之两 弧当两星，用纪限仪或弧矢仪测其两相距度分，得 径分。

系月高庳有四限：“一在本轮、次轮之两最高为极远； 二在两轮之两最庳为极近；三在本轮之高、次轮之 庳为中远；四在本轮之庳、次轮之高为中近。”各限之 径，而诸家所测多不等。极近，或曰三十三分，或曰三 十四乃至三十五分三十秒；中远、中近，或曰三十一 分，或曰三十二分三十五秒；极远，曰二十九分三十 秒。

问：“古今一月也，古今一仪也。诸名家所测，乃尔参差 何以故？”曰：“其故多矣。或人目有利钝不等，或夜有幽 明不等，或太空氤氲之气有清浊厚薄不等，是皆能 变易，视径为大小。”

其正法以月食为本。

本卷求日月径，多从歌白泥所测，葢取诸天，《验月历》 中，大都宗本其说。

第二题：《日月视径大小》。

图

古史记日食既者或言昼晦恒星皆见鸟栖兽宿或言月不尽掩日有金环系如中图月全掩日即其似径与日似径等此则食既于东生光于西既与甚同时不移晷也如右图月体不足掩日则有金环月之似径为小如三图则食

既以后，更有食甚，久而生光。月之似径为大，所以然 者，日在最高，月在本轮最庳，日高故视径小，月庳，故 视径大，则掩日有馀也。日在最庳，月在最高，日之视 径大，月小，则掩日不足也。俱在最高，俱在最庳，故两 视径等，则掩日适足也。

第三题：《日食时月视径之小大，随地不等》。

旧法于日全食时测定月之视径，随时不等。曰日在 最庳，月在最高，则两视径约皆三十一分，是以月掩 日为适足。若日高月庳，是日小月大，以月掩日则赢 矣。而或谓全食时有金环，是有时月小而日大，或曰 无之。此两说者，古来通士，疑弗能明也。至近今二十 年间，名历蔚兴，世济其美，辨义既晰，测候加精。因而 南北参订，然后乃知两《视径》随地各异，究极根缘，又 知日食时绝，难定视径之大小，遂使千年疑障，豁尔 蠲除。繇是观之，理弥析而愈有。智日出而靡涯，数甚 赜而难穷，岂可见限自封，谓“循古为已足哉。”

按“《总积》之六千三百一十四年”，为“万历二十九年辛 丑十二月。”〈建丑之月〉朔西士某者，苐谷之高第弟子也。于 诺物亚国，北极高六十四度有奇。本日未初刻测候， 得日全食、月掩日不足，四周都有金环，广寸许，约两 视径，为日大与月，小若六与五。于时推得日躔星纪 宫二度二十二分，是近最高。冲其视径当为三十一 分；月自行四度三十八分，是近最高，其视径亦当为 三十一分。依恒法，即两曜之视径。宜略等以相揜宜 适足。今实测为大小不等，若六与五。

同日，其同门刻《白尔》于玻厄米亚国北极出地五十 ○度有奇，则得月之视，径为三十分半，其相揜乃至 尽。

又总积之六千三百二十一年，为“万历三十六年戊 申八月。”〈建酉之月〉朔于某地北极高约五十一度，依法推 得日食六分之一，至期实测适合，是为两视径相等。 同日于某地北极高五十七度，推得日食十二分之 一有奇，至期实候悉不见食，是为日大月小，两视径 不等。

从上“两食”，两名士功力悉敌，秒分不爽，人所共信。密 推密测，无从得言。作用有差，而易地相方，乖违乃尔。 葢逾近北，日体逾大，月逾小；逾向南，日体逾小，月逾 大。以此见两视径不止随时大小，亦随地大小。又见 日食时未能得两视径之真率，又见日食分数未合， 不必尽因推步。然其故何也？

因之推本，其故有二：一曰蒙气差，一曰光体差。一者 清蒙之性，能令有光之体展小为大，如日月星出入 地时，本体皆见为大，其相距间亦见大；又如平面玻 璃镜以鉴物，则景较形为大；如轻云薄雾笼罩日体，

亦见为大：皆是也。今二史者，一在诺物，亚于《时日轨

图

高仅三度，又冬月地寒在海中，皆积气厚蒙之缘也。 故日体得展小为大，月无光则小于日。一在玻厄米 亚极，出地减前一十四度，又居平原，不迩江河湖海， 于时日轨高一十六度，蒙气已消，日体无繇得大，则 两视径等也，是一差也。二者月在日下，人目视之参 直，是生角体之形。其底月体，其末锐入于人之瞳心， 其周面则有光无光之界也。两界间蒙气愈厚，生光 愈多，其照耀之势，侵入于角体，则月之魄体能为小。 如图目与月与日相参，直依《推步法》两视径等，然自 目至月，其间有气，气映日生光，必越本界而侵入于 角体之限，人目遂不能全见月魄，故魄本非小，视之 若小。

系日食时，因气清浊，“为人见大小。”

二《系日食》之视分多寡，因去极远近。若本地去北极 近，则日轨庳，则气多，则分数少；去极远，则日轨高，则 气少，则分数多。

推步得数等，窥视即不等。

何者？《蒙》气多，日轨庳，熯湿之力，未获全成，即光大魄 小故也。日高者反是。

因上论“日之光，体人视之有时能为大；月之魄，体人 视之有时能为小。”近岁《名历》家既明其义，

《苐谷》之《遗书》，多所未竣，门人刻白，尔辈增修其业，日就精微。

因用视法。

依日轨高庳，论蒙气厚薄。

用测量法：〈推步定法〉立为“均数列表，以定日食时太阴、太 阳之视径”，从极出地二十○度至七十四度，或于太 阳用加差，或于太阴用减差，其理一也。表入《交食历》 中。

第四题《日月之视径》，与《实径大小绝异》。

是，其征有七。凡视径。〈与似径同〉“时见大，时见小”，必非其实 也，视也，一征也。即有时等，而日在上，去人远，月在下， 去人近，则日之实径必大，月必小，二征也。月掩日下 土所见九服各异如此。方此时日全食，南北相去四 五度。

二百五十里而一度

图

“即不见全食，东西同时亦不见全食。”是则月入地球 为小，地视日亦小，月视日更小，三征也。地景短，不能 食荧惑，何况岁星以上，则地小于日，月过地景则食， 食时见月，小于地景，则更小于日，四征也。七政各有 性情，能力施暨下土，其势略等。乃其视行有疾有迟。 行迟者，其天周大；人见为迟，本行自疾。所以然者，远 故也。近者行疾，其天周小，如舟行大水，远见行迟，近 见行疾，因是能力所施。近而疾者，其见功亟；远而迟 者，其见功缓：五征也。月距日九十度，其光过半圈，则 “发光之体大，受光之体小”，六征也。因上推月距地为 地全径者三十，日距地为地全径者六百○五，则日 天比月天其大。〈算周〉约二十倍日本天半度，月本天半 度，则其比例“为一”与二十七征也。

第五题：《月视地为小》；

义见前题《三征》《四征》。

第六题：“《月天》视《七政天》” 为小，去人最近。

曷知之？以交食知之。凡言食者，物在于彼，有他物隔 焉。或亏或蔽，则谓之食。所食者必远，能食者必近也。 所食者必在外，能食者必在内也。以球论，则内近心 者必小，外远心者必大也。试观月掩日，日为之食，日 外月内，不待言矣。月掩恒星，星为之食，星外月内，不 待言矣。独月与五星，历家言有时星食月，有时月食 星亦未然也。夫星固未始有在月下者也。历稽古史， 多言月食五星，而不言五星食月，斯著明已。今录略 如左：

月食辰星

一总积五千四百六十八年，为“唐元宗天宝十四年乙未十二月。”

月食太白

一总积五千五百五十○年，为“唐文宗开成二年丁 巳二月己亥日。”

《二》、本年七月丁亥日

三五千五百五十五年为“唐武宗会昌二年壬戌正 月。”

四、本年三月

五六千○五十五年为元顺帝至正二年壬午七月 乙未日。

月食荧惑

一五千五百二十五年为“唐宪宗元和七年壬辰正 月辛未”日。

二五千五百四十四年为“唐文宗泰和五年辛亥二 月甲申”日。

三六千○百二十七年为元仁宗延祐元年甲寅三 月壬申日。

月食岁星

一五千四百七十五年为“唐肃宗宝应元年壬寅正 月癸未”日。

二五千五百一十九年为“唐宪宗元和元年丙戌二 月壬申”日。

三：五千五百四十八年为“唐文宗泰和九年乙卯六 月庚寅”日。

四、本年十月庚申日

五五千五百五十二年为“唐文宗开成四年己未二 月丁卯”日。

月食填星

一五千五百四十一年为“唐文宗泰和二年戊申正 月庚午”日。

二五千五百四十五年为“唐文宗泰和六年壬子四 月辛未”日。

三六千○○七年为元世祖至元三十一年甲午九 月丙寅日。

第七题：《求月之实径》。

测月之实径用地径，古法也。今依《歌》“《白泥术》，月平。”〈两留〉 〈际〉距地度为三十地全径，又四之一，其视径三十二 分二十八秒，推算如左：

如图丁为地心乙，甲丙为月径三十二分，丁甲为月 距地三十，地全径成甲、丁、丙三角形，有角有边。求乙 丙，得千分地全径之二百七十六弱，为月全径。约之 得月，一地三倍有半强。若以周径法求之，则七。〈径也〉与 “二十一”，〈周也〉若六十　半地径。〈月天之半径〉与月天之周，依 法算，得一百九十。地径又七之一，以三百六十〈天周平度〉 而一，得一度，为三十六分地径之一十九。次以六十

图

分为一率〈六十分一度也〉三十六之一十九为二率，三十二分为三率，求得二千一百六十分地径之六百三十六，约得二十四之七或三有半之一，同上率。

若用月五限数所得大数同上零数小异不足算

若用《古多禄》某数，平距为四十九地半径，视径为三 十六分，算得月实径为千分地径之二百七十或二 百六十七，不合天验，今不用。

若用《苐谷》数，得千分之二百七十九，比歌《白泥》赢千 分之三，不足算。

第八题：《求日之实径》。

如左图，日距地为地全径者五百八十九有半，日视 径三十一分四十秒。〈歌白泥术〉即甲乙丁三角形，有乙直 角，有甲丁乙视角，有丁乙句，求甲乙股法，为全与五。

图

八九半若一十五分五十秒之切线与股〈日半径也〉算得二，又千万之七百一十五万一千一百九十一，半，径也。倍之，得五，又千万之四百三十○万二千三百八十二，约得日全径，为地全径者五又百分之四十三或五又半或又周径法求

之，所得数同。

第九题，“定日月实径各里数。”

“天度里差，古今不一。”今约定南北二百五十里而差 一度，以天周三百六十乘之，得九万里，求径，得二万 八千六百四十八里，以日径数。〈地一日五又百之四十三〉乘地径 之里数，得日之实径为一十五万五千五百六十五 里。月之实，径为地径千分之二百七十六。以乘地径 之里数，得七千九百○七里。

第十题：《求日体之容》。

《用测量全义》第六卷“法有径求周。”〈法以二十二乘径七而一〉得日

体周，为四十八万八千九百一十九里。求周之圜面 积。〈法以径乘周〉得七百五十六亿。〈数万至万曰亿〉五千八百六十 八万四千一百三十五里。求正面积，

大平圈之积也，法以周之圜面积，四而一。

得一百八十九亿一千四百六十七万一千○三十 四里。求其容。

法以径三之二乘大平圜之积，生球容之数。

得一千九百五十○万一千二百六十五亿三千三 百四十六万九千五百三十里，为日体之容积也。

“测体之里度” 者，乃实也。六面之体，各面一里。见《测量》六卷。

若以日体较地球之容，用上比例数。

地径一日径五又百之四十三。

其法置五有奇，再自之，得一百五十一，为“日体容地 球”之数。

若用《苐谷术》，

日距地为一千一百五十地半径，日视径，为三十一分。

地球径与日体径，为一与五，又六之一，置五又六之 一，再自之，得一百三十九有奇，为日体容地球之数。 较前术差一十二。若用《古多禄》某术，得七十六，不合 天，今不用。

第十一题：《求月体之容》。

月之实径与地球径，若二与七。

或六十分之一十七分九秒，或千分之二百八十六。

置两数，各再自之，得三百四十三与八。置三四，三八 而一，得四十三，为月一地四十三以求里数，同上法 依《苐谷》术，为四十二。

日、地、“月三容积” 之比例。

“月一地四十二，地，一日一百五十一”，以四十二乘一 百五十一，得六千三百四十二，为日体容月体之数 也。

因上法能推“日本天”，月本天可容地球之数。

《测月距地之高》第二十六。

用此法，可测日月五星去人远近度分，及自相距各 度分。

第一法：《两地并测》。

一“人在北，如顺天府”，北极出地三十九度五十五分。 〈十度〉测时，月在午正，得其距天顶设四十三度一十三 分，又一人在南与顺天府之地经度等数。

地球有南北度，如云北极出地若干度，南行二百五十里而减一度，北行加一度是也，名曰“地纬度。” 若两地同时刻而见月食，是两地同在一子午圈下，是东西经度也；赤道下，两地亦相去二百五十里而差一度，是名地经度。

如《广州府》。

《顺天府经度》，约在广州之东为五分刻之三，或赤道三度，高数甚大。不因此差，以为乖爽。

北极出地二十二度一十二分。测时，月在午正，得其 距天顶二十五度一十九分。

图丙

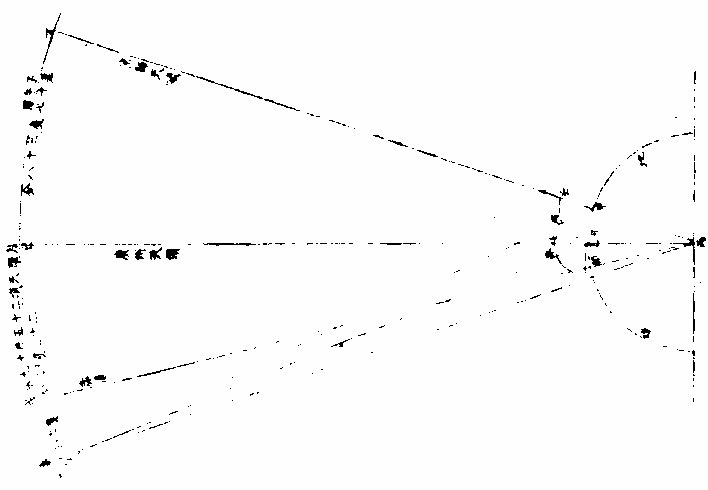
如图丙为地心，卯丑甲为地面，辛己丁为子午圈，戊 丙为赤道线。〈截球如简平仪法〉距赤道戊二十二度一十二 分为己，是广州之天顶，作己丙线，截地面于乙乙即 广州也。又距赤道戊三十九度五十五分为丁，是顺 天府之天顶，作丁丙线，截地面于甲甲，既顺天也。次 从甲从乙，作甲丑、乙卯，切地球之两线，为两府之各 地平线。两人在甲在乙各测月。作视线为甲，辛为乙， 辛作辛，丙为月距地心线，又作甲乙底线，今所求者， 辛丙也。

《法》甲乙丙角形，有甲丙乙丙两等腰。

俱地球之半径，俱为全数。

又有乙丙甲角，〈两地相距之度〉一十七度三十八分，“求甲乙 线。”

法有二：一用三角形法；一用通弦。甲乙线者，甲午乙弧之通弦也。

算得乙丙为十万，即甲乙为三○六、五、四。

次辛乙甲角形，有甲乙边，又有甲乙两角。何者？甲丙 乙形，丙角为一十七度三十八分，以减两直角一百八十度，馀甲乙两角并为一百六十二度二十四分， 平分之，得八十一度一十二分，为乙甲丙角。又先测 定己甲庚角四十三度一十三分，即两角并，得一百 二十四度二十五分，以减两直角，馀五十五度三十 五分，为乙甲庚角也。次以甲乙丙角八十一度一 十二分，减两直角，馀九十二度四十八分为甲乙壬 角。又先测定壬乙癸角二十五度一十九分，即两角 并为一百十八度○七分，为癸乙甲角也。以求辛 乙边法，引长辛乙边，作甲酉垂线，成甲酉乙直角形。

图

形有乙角为辛乙甲〈即癸乙甲〉角之馀有甲乙。求得甲酉边，又求得乙甲酉角。以井辛甲乙〈即庚甲乙〉角得辛甲酉角，又求得乙酉边。次甲辛酉直角形，有甲酉边，有甲角。求得辛酉边，去减乙酉，馀为所求辛乙边，得五四三四五○，约为五十四。

图

地半径

次辛乙丙角形有乙丙地半径〈即全数〉有辛乙边，又有辛乙丙角，何者？先得甲乙丙角八十一度一十二分，又得甲乙辛角一百二十四度○八分，并得二百○五度二十分，以减全周，得一百五十四度四十分，以

图

求丙辛边怯引长辛乙边从丙角作丙子垂线成乙子丙直角形形有丙乙边又有丙乙子角〈即丙乙辛角之馀〉二十五度一十九分。先求丙子及子乙，次辛丙子直角形，有丙子句，辛乙子股。求辛丙弦法，丙子辛子各自之，并而开方，得五五四

一约五十五地半径又十分之四强，为月距地心之 度也。

第二法本地自测

用月全食，于食甚时，测月轨高，又推太阳经度，以定 太阴经度。查高弧表或用测量。〈测量全义八卷〉法求月在本 时本经度之地平实高，与所测视高相减，为视差角， 则成三角形。其一边为地半径，一角为月视高角之 加角。〈本角外加一象限〉一为视差角法。求视馀角之对边，得 月距地若干。

“如西士”《玉山》王干。〈历学名家〉于总积六千一百七十四年， 为“天顺五年辛巳六月。”〈建巳之月〉某日亥正初刻。〈本地时刻〉月 食太阳躔鹑首宫九度三十四分三十四秒，月离星 纪同食甚。测月轨视高十七度半。又因本法，推日下 度，月实高度，俱一十八度三十一分。视实两高之较， 六十一分为视角之度分。

图己

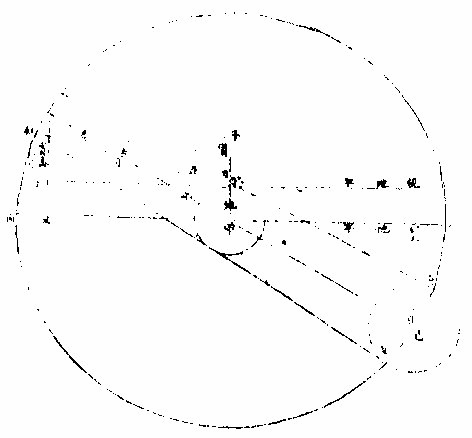
如右图，己为日，甲为地，壬为月，参直乙丙为实地平， 癸寅为视地平。测日在癸，视线为癸辰卯，视差角为 癸壬甲。癸壬甲形有癸甲。〈地半径全数〉有壬癸甲角。

午癸辰为“视高角” ，更加一象限，为壬癸甲角。

一百○七度三十○分，有癸壬甲。〈视差〉角：六十一分又 有癸甲壬角〈实高角丙甲戊之馀角〉七十一度二十九分求甲 壬边；

法曰：对角之正弦与对角之正弦。若角与角，置甲癸 全数为一算，得五十四有半，是本时月距地，为五十 四地半径又半弱。

第三法本地自测

用《日食》。西儒丁氏于总积六千二百八十○年，为“隆 庆元年丁卯四月。”〈建卯之月〉初九日午正。〈本地罗玛府时刻〉《时日 食测候》得日轨高五十九度一十分。食既，有金环。于 时日躔降娄宫二十八度三十八分，赤道北距一十 一度○一分四十一秒，本地极高四十一度五十○ 分二十○秒。因食既必地、月日相参直为一视线。随 用月历表及三视差法，推得月实距太阳二十九分

图

以加测高度〈五十九度一十分〉得五十九度四十二分四十四秒，为月之实高度分。如图甲为地心，乙为地面，为测目所在，己为月，丙为日，甲辛为实地平，庚为天顶。从地心过日心，作甲丙壬线，过月心，作甲己戊线。定日月两实高度。

或称辛壬弧，辛戊弧，或称其馀庚甲壬角，庚甲戊角。

又从目过日月心，作乙己丙丁线，定日月并距天顶 度，为庚丁弧或庚乙丁角，因成甲乙己三角形。形有 甲乙边，为地半径。有己甲乙角，为月实高之馀度。

实高，五十九度四十二分四十四秒。其馀三十○度一十三分一十六秒。

有甲乙己加角

所测之月视高度加一象限，共为一百四十九度一十分。

《求甲己边》：

有二角，自有第三角。其法两角之正弦与两角各对边比例等，

算得五十六地半径弱，为月距地心之度。

第四法本地自测

用月食恒星时：上以日食时推月之实高，测月之视 高立法。今以恒星立法，如总积六千一百九十九年， 为成化二十二年丙午，太阳躔大火宫六度三十分。

图

西史玉山王干晨见月周下切轩辕大星随时测得本星高四十五度本地极出地四十九度二十六分于时为卯正初刻月离鹑火二十二度四十○分在黄道北距二十六分有时有极高度有日躔有星高有月下周之视高

恒星之实高与“视高” ，为差极微。

有月之经度，纬度可得月之实高。

若以月心为实高。减月半径一十六分，得用下周，为实高。

“两高之差，以求月距地心”，如上法。

第五法

推月在黄平象限时，或推在南至时，或候午线时，测 其高，随时推其实纬度。两高加减，得视差之角。〈见前卷〉

测日距地之高。〈附：〉

图

第一法

用测月第一法

第二法

午正时测得日轨之视高随推其本时经度纬度得其实高两高相减得数为视差〈名地半径差〉或用《日躔历指图》，有地心，人目在地面，目在视地，平成三边直角

形，有目心边。〈地半径〉有“目心、日角。”

目见日出入时，其半在地平上，半在地平下，疑为初度分，非初度分也。为所见者视地平，非实地平也。其在中距，为差三分。最高二五四，最庳三○七。见《日躔表》。

求心日线法全数。〈内〉与目心边。〈外〉若日角之馀割线： 〈内〉与《日心线》。〈外〉算得一千一百四十五地半径，为日 距地心之度。若日在地平上，亦如在午法，一测一 推求视差。

第三法

用《月食》正法也。〈见上章。〉