钦定古今图书集成历象汇编历法典

　第一百十九卷目录

　算法部汇考十一

　　算法统宗七〈少广章第四中〉

历法典第一百十九卷

算法部汇考十一

《算法统宗七》

少广章第四中

立圆法歌

《立圆》问径法何如？十六乘积，九归除，除此数常为实 积，立方开见更何如？《立圆》：若问周围数，四十八乘积 数，躯乘为实，积用开立，即见周围数不虚。

法曰：外周者，置积若干，以四十八乘之，得若干为实， 以开立方法除之，得周。若要还原，以周自乘；再乘，以 四十八除之，见积问径。置积若干，以十六乘之，得 若干，又用九归之，得若干为实，以开立方法除之，得 径。若要还原，以径自乘；再乘，以九因十六除之，见 积周径下原有不尽者，或周径自乘、再乘，并入不 尽数周，以四十八除之，见积。径以九因十六除之，见 积若问周问径遇有馀积不尽者，依开立方下命 法命之。

“今有积六万二千二百零八尺，欲为《立圆》。”问“径若干？” 答曰：“径四十八尺。”

法曰：置积尺数，以十六乘之，又用九归之，得一十一 万零五百九十二尺，为实。以开立方法除之，初商四 十，自乘，得一千六百，再乘得六万四千，除实。馀实四 万六千五百九十二尺。另将初商四十以三因，得一 百二十为方法，列位次商八尺于初商之次，得四十 八尺，就以八乘之，得三百八十四尺，为廉法。以方乘 廉，得四万六千零八十尺，除实。馀实五百一十二。另 以次商八尺自乘，再乘，得五百六十二尺，为隅法。除 实恰尽，得立圆径。合问。

此问周径如圆球

“今有积六万二千二百零八尺，欲为立圆。”问“周若干？” 答曰：“周一百四十四尺。”

法曰：置积尺，以四十八乘之，得二百九十八万五千 九百八十四尺，为实。以开立方法除之，初商一百尺， 自乘，得一万，再乘，得一百万，除实，馀实一百九十八 万五千九百八十四尺。另以初商一百，以三因，得三 百为方法。次商四十于初商之下，共一百四十，就以 四十乘之，得五千六百，为廉法。以方乘廉，得一百六 十八万，除实馀实三十万零五千九百八十四。另以 次商四十自乘，再乘，得六万四千，为隅法。除实，馀实 二十四万一千九百八十四。再以初次商一百四十， 以三因，得四百二十，为方法。再商四尺于初次商之 下，共得一百四十四尺。就以四尺因之，得五百七十 六，为廉法。以方乘廉，得二十四万一千九百二十，除 实，馀实六十四。又以再商四尺自乘，再乘得六十四， 除实讫，合问。

凡立圆问周径，遇数单者，则有不尽。

今有立方积一万五千六百二十五步，问“立方一面 若干？”

答曰：“二十五步。”

归除《开立方法》曰：“置积一万五千六百二十五尺为 实，以万积商二十置于积前，就置二十于右下，自乘， 得四百步，与上商二十”相呼，二四除实八千，馀实七 千六百二十五步，却以右下四百步，以三十乘之，得 一千二百为法，归除之呼逢五进五，又呼二五，除一 千。另置初商二十步，以次商五步乘之，得一百步，以 三因之，得三百步。以加入自乘次商五步，得二十五 步，共三百二十五步。于右与次商五步相呼，除之，呼 三五除一千五百步，又二五除一百步，又五五除二 十五步，积尽。以左上二十五步为立方一面之数。《合 问》。

今有《立方》积一亿零二百五十万零三千二百三十 二尺，问“立方一面若干？”

答曰：“四百六十八尺。”

《归除开立方法》曰：“置积为实。”以七千万该商四百尺 于左上，又置四百尺于右下，自乘，得一十六万，相呼， 一四除，四千万尺，又四六除二千四百万，馀实三千 八百五十万零三千二百三十二尺，却以右下一十 六万尺，以三乘之，得四十八万为法。归除之，呼四三 七十二少除。〈因下位数不足除〉呼，四归起一，下还四呼，六八 除四十八。另置初商四百尺，以次商六十尺乘之，得 二万四千尺，以三因之，得七万二千尺，为廉法。加入 次商六十尺，自乘，得三千六百尺，共七万五千六百尺。却以次商六十尺相呼除之，六七除四十二，又五 六除三十，又六六除三十六。馀实五百一十六万七 千二百三十二尺。以方法四十八万，并入两个廉法 七万二千，再并入隅法三个三千六百尺，共得方法 六十三万四千八百尺为法。归除之。呼六五，八十二， 呼三八，除二十四，又呼四八，除三十二，又八八，除六 十四。右下之法不用。再置所商共四百六十尺，以次 商八尺乘之，得三千六百八十尺，以三因之，得一万 一千零四十尺，并入，再商八尺，自乘，得六十四尺，共 一万一千一百零四尺。又以次商八尺相呼除之，一 八除八万，又一八除八千，又一八除八百，又四八除 三十二尺。除实恰尽。以左上所商四百六十八尺，为 立方一面之数。《合问》：

开立方带纵法

今有方仓贮米五百一十八石四斗，方比高多三尺， 问方高各若干？

答曰：“方一丈二尺，高九尺。”

法曰：置米五百一十八石四斗，以《斛法》二尺五寸乘 之，得积一千二百九十六尺为实。以开立方带纵除 之，以方多三尺自乘，得九尺，为纵方。再置三尺倍之， 得六尺，为纵廉。约积一千商十尺。今有纵方，只商九 尺，置于实前，另以九尺自乘，得八十一尺，加入纵方 九尺，共九十尺，为方法。另以纵廉六尺，以九尺乘之， 得五十四尺，为廉法。二法并共一百四十四尺。于右 下以所商九尺相呼，一九除九，又呼四九除三十六， 又四九除三十六，除实恰尽。以商九尺为高，加入方 多三尺，得方仓一十二尺。《合问》

今有立方一所，积一千七百八十七万五千尺，只云 高阔相等，长多阔三十六尺。问立方高阔及长若干？ 答曰：“长二百八十六尺，阔二百五十尺，高二百 五十尺。”

法曰：置积一千七百八十七万五千尺为实。以开立 方带纵法除之，初商约得二百尺，自乘，得四万尺，再 乘得八百万尺。又约二百五十尺自乘，得六万二千 五百尺，再以二百五十尺乘之，得一千五百六十二 万五千尺，减去积馀，积二百二十五万尺为实。另置 长多三十六尺，以所商二百五十尺乘之，得九十尺， 再以二百五十尺乘之，得二百二十五万尺，除实恰 尽，得阔二百五十尺，加入长多三十六尺，共二百八 十六尺，为长数。《合问》。

今有立方积二万九千八百零八尺，高比方不及一 丈三尺，问高方各若干？

答曰：“高二丈三尺，方仓三丈六尺。”

法曰：置积二万九千八百零八尺为实。以开立方带 纵法除之，约实二万。商三十尺自乘，得九百尺。再以 三十尺乘之，得二万七千尺。又约商三十六尺自乘， 得一千二百九十六尺。另置三十六尺，减不及一十 三尺，馀二十三尺乘之，得二万九千八百零八尺。除 实尽，得方仓三十六尺，高二丈三尺。合问。

今有三乘方积二千零一十五万一千一百二十一 尺，问：“一面若干？”

答曰：“六十七尺。”

法曰：置积为实。下法常超三位，初商六十于左，下法 亦置六十自乘，得三千六百，再乘得二十一万六千， 为隅法。与上商六十相呼，除实一千二百九十六万， 馀实七百一十九万一千一百二十一尺。乃以四乘 隅法二十一万六千，得八十六万四千，为方法。另置 上商六十自乘，得三千六百，又以六因之，得二万一 千六百尺，为上廉。又置上商六十，以四乘，得二百四 十尺，为下廉。次商七尺于左，六十之。次下法亦置七 尺，自乘，得四十九尺，再以七因，得三百四十三尺，为 隅法。又以次商七尺乘上廉二万一千六百，得一十 五万一千二百。又以下廉二百四十，用两次七因初 次因，得一千六百八十尺，二次因得一万一千七百 六十尺。以方法八十六万四千，上廉一十五万一千 二百，下廉一万一千七百六十，隅法三百四十三，并 四法共一百零二万七千三百零三尺，皆与次商七 尺相呼，除实恰尽得一面六十七尺。合问：〈此三乘方捷径〉 一法：用二次开平方法除之，亦得。初一次置积数为 实，以开平方法除之，商得四千四百八十九尺。第二 次就以此初商数为实，亦以开平方法除之，即得一 面六十七尺。《合问》：〈此又捷径〉

若还原，置一面六十七尺，自乘，得四千四百八十九 尺，再乘，得三十万○○七百六十三尺，又乘之，即见 原积数也。

自乘，再乘又乘，故曰“三乘。”其四乘乃四次乘也。其五 乘，乃五次乘也。

今有田积三千三百七十五尺。问“立方面若干？” 答曰：“面方一十五尺。”

法曰：置积三千三百七十五尺为实，以开立方法除 之。古法用三为廉率，约实定位，从实。末位尺十尺定尺，百尺，千尺定十尺。初商一十于左。下法，亦置初商 一十自乘，得一百，再乘得一千，除实讫，馀实二千三 百七十五尺。却以下法，初商一十自乘，得一百，用三 因为方法。又以初商一十，以三因，得三十，为廉。次商 五尺于左。初商之次，下法亦置。次商五尺自乘，得二 十五尺，为隅法。又以次商五尺乘廉三十，得一百五 十，为廉法。并方法三百，廉法一百五十，隅法二十五， 共四百七十五尺，皆与次商五尺相呼。四五除二，五 七除三十五，五五除二十五，得方面一十五尺。《合问》。

<h3 id="开立方�" style="text-align: center">开立方�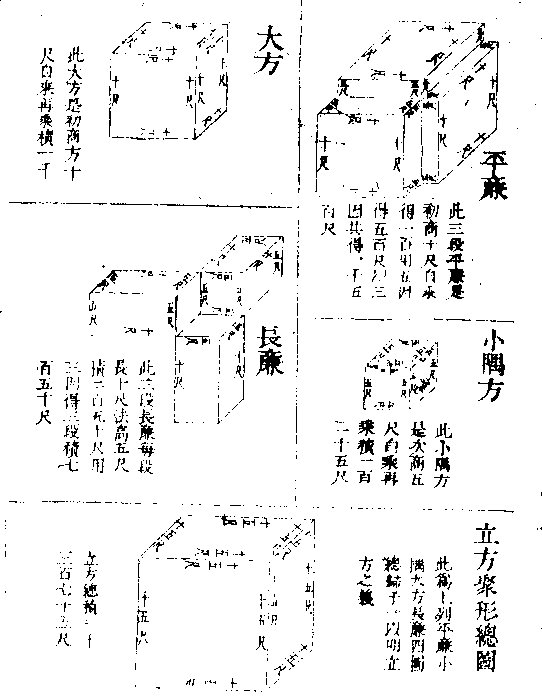

大段。解曰：“立方积，形如骰子，有上下、左右、前后六面， 方如一段。大方积，是初商方高十尺。”自乘，再乘，得一 千尺。三段平廉，每段方十尺，高五尺，即初商十尺。自 乘，又以次商五尺乘，积五百尺，用三因，即三段积一 千五百尺。三段长廉，每段长十尺，阔五尺，高五尺，即 初商十尺。以次商五尺乘，又以次商五尺乘，得每段 积二百五十尺。用三因，即三段积七百五十尺。一段 小方隅，即次商五尺。自乘，再乘，积一百二十五尺也。

《求米仓窖盛贮歌》：〈每石斛法二尺五寸。〉

“米求仓窖要知源，斛法先除米数全。若见圆仓乘十 二方窖三，因米数然。三十六乘圆窖米，各为实积定 无偏，却用立方开”见约方求长、阔约为先，圆数求周 为约数，各将约数自乘焉。乘来为法除实积，便见深 高法更元。

今有米二千四百一十九石二斗，欲为方仓盛之，问 长、阔、高各若干？

答曰：“长二十八尺，阔一十八尺，高一十二尺。”

法曰：置米数，以斛法二尺五寸乘之，得六千零四十 八尺为实。以开立方法约之，得阔一十八尺，便约长 二十八尺。却以长阔相乘，得五百零四尺为法。除实， 得高合问。

今有米七百零五石六斗，欲作圆仓盛之问周围及 高各若干？

答曰：“周四十二尺，高一十二尺。”

法曰：置米数，以斛法二尺五寸乘之，得一千七百六 十四尺，再以圆法十二乘之，得二万一千一百六十 八尺，为实。以开立方法约之，得周四十二尺，自乘，得 一千七百六十四尺为法。除实，得高一十二尺。合问 今有米五百七十七石二斗，欲作方窖盛之，问上下 方及深各若干？

答曰：“上方九尺，下方一十二尺，深一十三尺。”

法曰：置米数，以斛法二尺五寸乘之，得一千四百四 十三尺。又以三因之，得四千三百二十九尺，为实。以 开立方法约之，得上方九尺，便约下方一十二尺。却 以上方自乘，得八十一尺。另以下方自乘，得一百四 十四尺。又以上方九尺乘下方一十二尺，得一百零 八尺。并三位，共三百三十三尺为法。除实，得深一十 三尺，合问：

今有米七十七石二斗，欲作圆窖盛之问上下周及 深各若干。

答曰：“上周一十四尺，下周一十八尺，深九尺。”

法曰：置米数，以斛法二尺五寸乘之，得一百九十三 尺。再以圆率三十六乘之，得六千九百四十八尺为 实。以开立方法约之，得上周一十四尺，便约下周一 十八尺。另以上周一十四尺自乘，得一百九十六尺。 又以下周一十八尺自乘，得三百二十四尺。又以上 周一十四乘下周一十八，得二百五十二尺。并三位 共七百七十二尺为法，除实得深九尺。《合问》：

今有米二千四百一十九石二斗，欲造长仓盛之，只 云“阔一十八尺，高一十二尺，问长若干。”

答曰：“长二十八尺。”

法曰：置米数，以斛法二尺五寸乘，得六千零四十八 尺为实。另以高乘阔，得二百一十六尺为法。除实，得 长合问。

或只云“长二十八尺，高一十二尺。”问：“阔若干？”

答曰：“阔一十八尺。”

法曰：仍以前实，却以长高相乘，得三百三十六尺为 法。除实，得阔一十八尺。合问。

今有米七百零五石六斗，欲作圆仓盛之，只云“高一 十二尺，问周若干。”

答曰：“周四十二尺。”

法曰：置米数，以斛法二尺五寸乘之，得一千七百六 十四尺。又以圆率十二乘之，再以高一十二尺除之如故为实。以开平方法除之，得周四十二尺。合问 今有米五百七十七石二斗，欲作方窖盛之，只云“上 方九尺，深一十三尺。问下方若干？”

答曰：“下方一十二尺。”

法曰：置米数，以斛法二尺五寸乘之，得一千四百四 十三尺；以三因之，得四千三百二十九尺。以深一十 三尺除之，得三百三十三尺。内减上方，自乘，得八十 一尺，馀二百五十二尺为实；以上方九尺为纵方。开 平方法除之，得下方一十二尺。合问。

或云：“下方一十二尺，深一十三尺。”问：“上方若干？” 答曰：“上方九尺。”

法曰：仍以前实四千三百二十九尺，以深除之，得三 百三十三尺。内减下方自乘一百四十四尺，馀一百 八十九尺，为实。以下方一十二为纵方。以开平方法 除之，得上方九尺。《合问》。

今有米七十七石二斗，欲造圆窖盛之，只云“上周一 十四尺，深九尺，问下周若干。”

答曰：“下周一十八尺。”

法曰：置米数，以斛法二尺五寸乘之，得一百九十三 尺。又以圆率三十六尺乘之，得六千九百四十八尺。 以深九尺除之，得七百七十二尺。内减上周，自乘一 百九十六尺，馀五百七十六为实。以上周一十四为 纵方。以开平方法除之，得下周一十八尺。《合问》： 或云：“下周一十八尺深九尺，问上周若干？”

答曰：“上周一十四步。”

法曰：仍以前实六千九百四十八尺，以深九尺除之， 得七百七十二尺。内减下周自乘，得三百二十四尺。 馀四百四十八尺为实。以下周一十八尺为纵方。以 开平方法除之，得上周一十四尺。《合问》。

今有米五百一十八石四斗，欲造方仓，盛之问“方、高 各若干？”

答曰：“方一十二尺，高九尺。”

法曰：置米数，以斛法二尺五寸乘之，得一千二百九 十六尺为实。以开立方法约之，得方一十二尺。却以 方一十二尺自乘，得一百四十四尺为法。除实，得高 九尺。合问。

或云“高九尺，问方若干。”

答曰：“方一十二尺。”

法曰：仍以前实以高九尺除之，得一百四十四尺。以 《开平方法》除之，得方一十二尺。合问。

分田截积法上

直田截积歌

《直田》截积法尤奇，截长积步阔除之，截阔用长除且 易，得其步数不须疑。

法曰：“若依原长截积，则以原阔除之。若依原阔截积， 则以原长除之。”

直田截积原载《方田章》，因与圭梯等截积间隔，不便观览，今移此以统于一。

今有直田，长四十八步，阔四十步。今依原长截积七。

直田截阔图

百二十步，问：“截阔若干？”

答曰：“阔一十五步。”

法曰：置截积七百二十步为实，以原长数为法除之，即得截阔数。《合问》：

今有直田，长四十八步，阔四十步。今依原阔截积七 百二十步，问截长若干？

直田截长图

答曰：“长一十八尺。”

法曰：置截积七百二十步为实，以原阔四十步为法，除之，得截长一十八步。合问。

今有方田一丘，要“从东南角截一直形积三十二步， 南边阔四步，问截东边长若干？”

答曰：“截东长八步。”

《法》曰：置截积三十二步为实，以南阔四步为法除之。

方田截直图

得截积东长八步。《合问》：若东长定数，问截南阔，就以长数为法而除截积。

今有直田，长一十五步六分，阔一十二步。今从东边。

直田截斜图

截积五十四步六分。北头要阔四步，问截南头阔若干？

答曰：“截南头阔三步。”

法曰：置截积五十四步六分为实。以

原长一十五步六分为法，除之，得截阔三步五分，此 是二广均匀之数。加倍得七步，减去北广四步，馀得 截南广三步是也。

又法，倍截积，得一百零九步二分为实。以原长一十 五步六分为法，除之，得共截阔七步减北广四步，馀 得截南广三步亦得。

今有直田，长一十五步，阔一十二步。今从西北《角截》。

直截句股图

句股形一段，积三十一步五分，原坐落西边，股长九步，问截北边句阔若干。

答曰：“截北句，阔七步。”

法曰：置截积三十一步五分，倍之，得六十三步，以西 股长九步为法，除之，得截北句阔七步。合问。

今有直田，积一千九百二十步，只云“长六十步，问阔 若干？”

答曰：“阔三十二步。”

法曰：置积一千九百二十步为实，以长六十步为法 除之，得阔。若是只云阔三十二步，问长若干，就以 阔为法除之，即得长。

今有圭田，积二百二十五步，只云“长三十步，问阔若 干？”

答曰：“阔一十五步。”

法曰：置积倍之，得四百五十步为实，以长为法除之， 得阔。若云中长步数，倍积为实，以阔为法除之，即 得。

以上二款，名曰“忘长失短” ，与“直田截积” 意同。

今有句股田，长三十步，阔一十五步。今从尖截长一 十二步，问中广若干。

勾股截积图

答曰：“截中广六步。”

法曰：置截长一十二步，以句阔乘之，得一百八十步为实，以股长为法除之。

又法：置句为实，以股为法除之，每股长一步，得阔五 分。以乘截长亦得。

今有斜田，南广四步，北广十二步，长三十二步。今“从 中截腰广六步，问截南长若干？”

答曰：“截南头长八步。”

斜田截积图

法曰：置截中广六步，减上广四步，馀二步，以乘长三十二步，得六十四步为实。却将南北二广相减，馀八步为法，除之，即得。若截下长。

置下广，减中广，馀六步。以乘原长，得一百九十二步 为实。以上下二广相减，馀八步为法，除之，得截下长 二十四步。《合问》。

今以前图截下长二十四步，问截中广若干？

答曰：“六步。”

法曰：将下广减去上广四步，馀八步为实。以原长三 十二步为法除之，每长一步，得阔差二分五釐。就以 此为法，以乘下长二十四步，得阔差六步。以减下阔 一十二步，馀六步，即是中广合问。

今有梯田，积一千五百步，北广四十步，中长五十步， 问南广若干？

答曰：“南广二十步。”

法曰：置积一千五百步，倍之，得三千步为实。以长五 十步为法，除之，得六十步，于内减北广四十步，馀得 南广二十步。《合问》：

原有斜田，南广四步，北广十步，长一十二步。今欲增 作句股样式，问股长出若干？

斜增为勾股图

答曰：“股长出八步。”

法曰：以南广四步乘长一十二步为实，另以二广相减，馀六步为法，除之，得尖出股长八步。合问。

《圭求广纵歌》。〈除《圭尖》即是梯形。〉

梯求上广出尖长，上阔乘纵法最良，却将上下广相 减，馀法除之免思量。

今有上圭下梯田，上广一尺六寸，下广一十二尺八

圭求广纵图

寸圭下正纵一十尺零五寸，问圭尖长若干。

答曰：“尖高长一尺五寸。”

《法》曰：“置正纵一十尺零五寸以上。”

广一尺六寸乘之，得一十六尺八寸为实。另以下广 一十二尺八寸减上广一尺六寸，馀一十一尺二寸 为法，除之，得圭尖长一尺五寸。《合问》。

圭求下广歌

圭田若问《梯》下广，圭梯并长，不必想上广乘长为实， 则尖长法除，即下广。

法曰：置圭长并梯长共一十二尺以上，广一尺六寸 乘之，得一十九尺二寸为实。以尖长一尺五寸为法， 除之，得下广一十二尺八寸合问。

圭求外梯长歌

圭田：欲问外梯长，下广减去，上广，良除，以圭长乘为 实。上广法除，是梯长。

法曰：以下广一十二尺八寸，减去上广一尺六寸，馀 一十一尺二寸。以圭长一尺五寸乘之，得一十六尺 八寸为实。以上广一尺六寸除之，得梯正纵长一十 尺零五寸合问。

圭求中广歌

《圭》求中广要思量，却用下《广》乘，尖长正纵，加入尖长 数为法，除之中广良。

法曰：置下广一十二尺八寸，以尖长一尺五寸乘之， 得一十九尺二寸为实。另以正纵一十尺零五寸加入尖长一尺五寸，共一十二尺为法，除之，得中广一 尺六寸。合问。

假如三角田一丘，三面各一十四步，今作三假，俱要 四角，问长阔各若干？

三角截四角圆

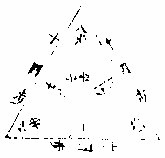
答曰：共积八十四步，三角各得二十八步，每角计长八步，阔七步。法曰：置每面一十四步，六因七归，得中径一十二步。另以每面一十四步与径一十二步相乘，得一百六十八。

步折半，得积八十四步，为实。以三段归之，各得二十 八步。却以每面折半，得阔七步，以归二十八步，得四 步，倍之，得中长八步。《合问》：

今有直田，长一十五步，阔一十二步。今依《阔截圭积》。

直田截圭图

四十五步问截圭长若干？答曰：“圭长七步五分。”

法曰：置截积，倍之，得九十步为实，以阔一十二步为法，除之，即得其馀。

圭梯等截法。俱用开方列法于左：

“圭田截积”歌：〈若作三段分者，先截尖段下二段，以作《梯形截法》。〉

《圭田》截积小头知倍积原长以乘之，原阔归除为实 积开方便见截长。宜仍以截长乘原阔，原长为法以 除之，除来便见截阔数，法明简易不须疑。

今有圭田，长七十五步，北阔三十步。今自《尖头截积》

圭截小头圆

四百零五步。问截长阔各若干？答曰：“长四十五步，阔一十八步。” 法曰：置截积四百零五步，倍之，得八百一十步。以原长七十五步乘

之，得六万零七百五十步，以阔三十步除之，得二千 零二十五步为实，以《开平》方法除之，得截长四十五 步。就以原阔三十步乘之，得一千三百五十步为实， 以原长七十五步为法，除之，得截阔一十八步。《合问》： 今有句股田，股长四十步，句阔二十步。今从大头截。

勾股截积图

积一百七十五步，问“所截长、阔各若干？”

答曰：“截下长一十步，截上广一十五步。”

法曰：先将句股相乘，得八百，折半得积四百步。减截 积一百七十五步，馀积二百二十五步，以作圭田截 积小头，知而算之，置小头积二百二十五步，倍作四 百五十步，以原长四十步乘之，得一万八千步，以原 阔二十步除之，得九百步，为实。以《开平方法》除之，得 上尖长三十步。就以此为法，以除倍积四百五十步， 得截阔一十五步。另将原长减去截长三十步，馀得 下长一十步。《合问》。

今又有圭田，长七十五步，北阔三十步。今自“北《阔截》。”

圭截大头图

积七百二十步。问截长阔各若干？答曰：“截下长三十步，阔一十八步。”

法曰：置截积七百二十步倍之，得。

一千四百四十步。以原阔三十步乘之，得四万三千 二百步为实，以原长七十五步为法，除之，得五百七 十六步。再以北阔三十步自乘，得九百步，以减五百 七十六步，馀三百二十四步为实，以开平方法除之， 得截阔一十八步，并北广三十步，共四十八步，折半 得二十四步为法。除截积七百二十步，得截长三十 步，合问。